Seminar presentation on Gaussian polynomials
Research Overview
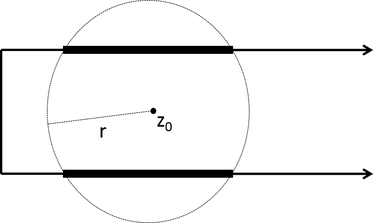
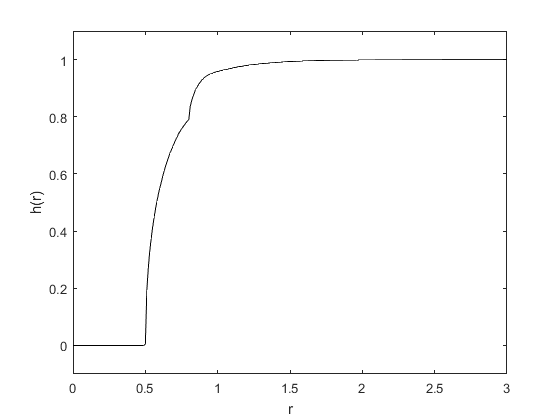
My current research focus is in computational analysis in the study of harmonic measure in complex domains. By placing a randomly-moving Brownian particle in a complex domain, then determining the probability the particle will first hit the boundary of the domain within some fixed distance r from the base point z0, one can construct the harmonic measure distribution function (h-function) in order to determine both geometric and analytic information about the domain.
|
|
This past summer, I worked with Oberlin student Miranda Schaum in constructing h-functions of domains by simulating Brownian motion inside of the domains. We discovered that by implementing teleportation, a process in which particles take large random steps to move about the domains, into our simulation programs, we were able to increase their computational efficiency while still giving information about the structure of the domains. We wrote a paper earlier this fall that was accepted by MCURCSM for presentation, and we will be presenting our work at conferences in the coming months. We plan to publish another paper this spring for journal publication.
I am also working with my thesis advisor, Dr. Mio Iovanov, in the area of representation theory. Our work has been to classify representation rings of Hopf algebras in order to determine how the representations of these Hopf algebras interact via direct sums and tensor products. Many of these representation rings have been classified in recent years for finite-dimensional Hopf algebras such as the Taft algebras and Sweedler's 4-dimensional Hopf algebra using modules. My work studies the representation rings of infinite-dimensional Hopf algebras using their comodule representations rather than their modules. As a result of my work, I have mastered the art of drawing multiplication tables.
|
Documents:
|
In addition, here are materials I have designed for a course based on my research area, Mathematical Quivers:
| ||||||||||||